Trong bài viết này Blog tuicocach.com sẽ giới thiệu tới các bạn thuật toán sắp xếp trộn(Merge Sort). Đây là một trong các thuật toán sắp xếp căn bản thường dùng.
DANH SÁCH BÀI VIẾT Thuật toán sắp xếp nhanh (Quick Sort) Thuật toán sắp xếp trộn (Merge Sort) Thuật toán sắp xếp đổi chỗ trực tiếp (Interchange Sort) Thuật toán sắp xếp nổi bọt (Bubble Sort) Thuật toán sắp xếp chọn(Selection Sort) Thuật toán sắp xếp chèn (Insertion sort)
Ý tưởng của thuật toán Merge Sort
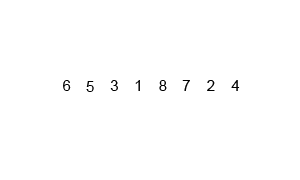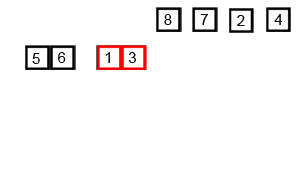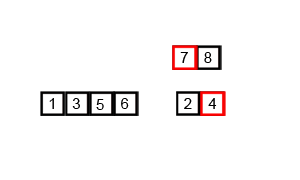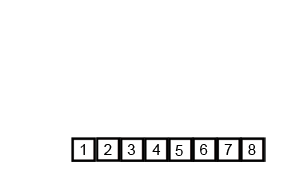
Sắp xếp trộn (merge sort) là thuật toán một ví dụ tương đối điển hình của lối thuật toán chia để trị.
- Chia (Divide): Chia dãy gồm n phần tử cần sắp xếp thành 2 dãy, mỗi dãy có n/2 phần tử.
- Trị (Conquer): Sắp xếp mỗi dãy con một cách đệ quy sử dụng sắp xếp trộn. Khi dãy chỉ còn một phần tử thì trả lại phần tử này.
- Tổ hợp (Combine): Trộn (Merge) hai dãy con được sắp xếp để thu được dãy được sắp xếp gồm tất cả các phần tử của cả hai dãy con.
Thuật toán chia:
Giả sử ta có dãy L ban đầu gồm n phần tử là L[0].....L[n-1].
- Chia dãy L gồm n phần tử thành 2 dãy con, mỗi dãy có n/2 phần tử, chia tiếp dãy con n/2 phần tử thành n/4 phần tử. Lặp lại quá trình cho đến khi mức chia tối thiểu có nghĩa mỗi dãy con chỉ bao gồm 1 phần tử duy nhất.
- Thuật toán chia kết thúc khi ta có n dãy con chỉ bao gồm duy nhất một phần tử, lúc này ta coi n dãy con chỉ bao gồm 1 phần tử đó là n dãy đã sắp xếp.
XÊM THÊM Thuật toán sắp xếp chọn(Selection Sort) Thuật toán sắp xếp chèn (Insertion sort) Thuật toán sắp xếp nổi bọt (Bubble Sort)
Ý tưởng triển khai code:
mergeSort(int arr[], int l, int r)
if (l < r)
// 1. Tìm chỉ số nằm giữa mảng để chia mảng thành 2 nửa:
// middle m = (l+r)/2
// 2. Gọi đệ quy hàm mergeSort cho nửa đầu tiên:
// mergeSort(arr, l, m)
// 3. Gọi đệ quy hàm mergeSort cho nửa thứ hai:
// mergeSort(arr, m+1, r)
Thuật toán trộn:
Giả sử có hai dãy đã được sắp xếp L[1..n_1n1] và R[1..n_2n2]. Ta có thể trộn chúng lại thành một dãy mới M[1..n_1 + n_2n1+n2] được sắp xếp theo cách sau:
- So sánh hai phần tử đứng đầu của hai dãy, lấy phần tử nhỏ hơn cho vào dãy mới. Tiếp tục như vậy cho tới khi một trong hai dãy rỗng.
- Khi một trong hai dãy rỗng, ta lấy phần còn lại của dãy kia cho vào cuối dãy mới.
Ý tưởng triển khai code:
- Kiếm tiền Accesstrade, kiếm tiền tại nhà với Accesstrade.vn – Tiếp thị liên kết
- MegaURL – Rút gọn link kiếm tiền có giá cao tại Việt Nam
- Top những App kiếm tiền online trên điện thoại tốt nhất hiện nay
//Trộn 2 mảng con vào mảng mới cho tới khi 1 trong 2 mảng con rỗng
while (i < n1 && j < n2)
{
if (L[i] <= R[j]) //Nếu phần tử đầu của dãy L <= phần tử đầu dãy R
{
// 1.Lấy phần tử đầu tiên của dãy L cho vào cuối của dãy mới.
// 2.Tăng phần tử thứ 2 của dãy L thành phần tử đầu tiên
}
else //Nếu phần tử đầu của dãy L > phần tử đầu dãy R
{
// 1.Lấy phần tử đầu tiên của dãy R cho vào cuối của dãy mới.
// 2.Tăng phần tử thứ 2 của dãy R thành phần tử đầu tiên
}
//1.Tăng kích thước của mảng mới
}
//Nếu dãy L không rỗng, lấy phần còn lại của dãy L cho vào cuối dãy mới.
while (i < n1)
{
// 1.Lấy phần tử đầu tiên của dãy L cho vào cuối của dãy mới.
// 2.Tăng phần tử thứ 2 của dãy L thành phần tử đầu tiên
// 3. Tăng kích thước của mảng mới;
}
//Nếu dãy R không rỗng, lấy phần còn lại của dãy R cho vào cuối dãy mới.
while (j < n2)
{
// 1.Lấy phần tử đầu tiên của dãy R cho vào cuối của dãy mới.
// 2.Tăng phần tử thứ 2 của dãy R thành phần tử đầu tiên
// 3. Tăng kích thước của mảng mới;
}
Ví dụ sử dụng thuật toán Merge Sort sắp xếp dãy {38, 27, 43, 3, 9, 82, 10} ta có toàn bộ sơ đồ tiến trình của thuật toán từ lấy từ wikipedia như sau nhé:
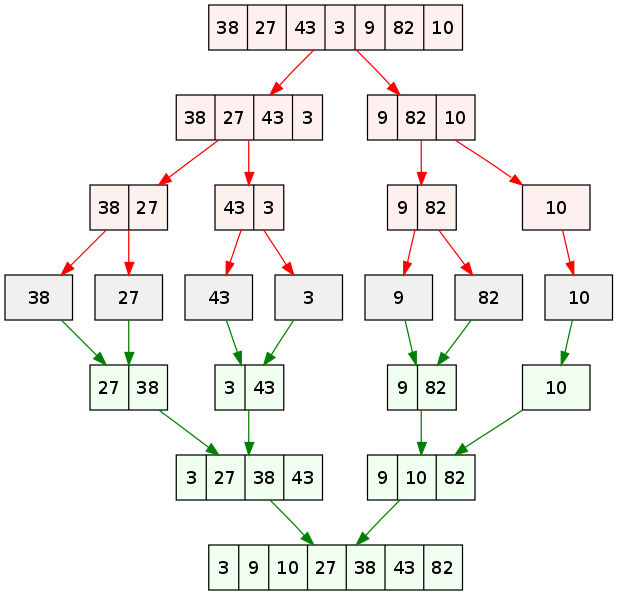
Nhìn kỹ hơn vào sơ đồ này, chúng ta có thể thấy mảng ban đầu được lặp lại hành động chia cho tới khi kích thước các mảng sau chia là 1. Khi kích thước các mảng con là 1, tiến trình gộp sẽ bắt đầu thực hiện gộp lại các mảng này cho tới khi hoàn thành và chỉ còn một mảng đã sắp xếp.
Cài đặt thuật toán Merge Sort trên C/C++
#include<stdlib.h>
#include<stdio.h>
void merge(int arr[], int l, int m, int r)
{
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
//Tạo 2 mảng tạm con
int L[n1], R[n2];
/* Copy dữ liệu sang các mảng tạm */
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
i = 0; // Khởi tạo chỉ số bắt đầu của mảng con đầu tiên
j = 0; // Khởi tạo chỉ số bắt đầu của mảng con thứ hai
k = l; // Khởi tạo chỉ số bắt đầu của mảng lưu kết quả
/* Trộn hai mảng tạm vừa rồi vào mảng arr*/
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
//Lấy phần còn lại của dãy L cho vào cuối dãy arr nếu còn.
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
//Lấy phần còn lại của dãy R cho vào cuối dãy arr nếu còn.
while (j < n2)
{
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
//Tìm chỉ số nằm giữa mảng để chia mảng thành 2 nửa:
int m = l+(r-l)/2;
// Gọi hàm đệ quy tiếp tục chia đôi từng nửa mảng
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
//Gọi hàm trộn
merge(arr, l, m, r);
}
}
// Hàm xuất mảng
void printArray(int A[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", A[i]);
printf("\n");
}
int main()
{
int arr[] = {12, 11, 13, 5, 6, 7};
int arr_size = sizeof(arr)/sizeof(arr[0]);
mergeSort(arr, 0, arr_size - 1);
printf("\nSorted array:\n");
printArray(arr, arr_size);
return 0;
}
Kết quả chạy thực hiện chương trình trên:
5 6 7 11 12 13Đánh giá thuật toán sắp xếp Merge sort
Không gian bộ nhớ sử dụng: O(n)
Độ phức tạp thuật toán
- Trường hợp tốt: O(nlog(n))
- Trung bình: O(nlog(n))
- Trường hợp xấu: O(nlog(n))

Bình luận