Bạn đang sắp hoặc sẽ thi Olympic tin học sinh viên Việt Nam, vậy hãy thăm khảo qua đề thi chính thức Olympic tin học sinh viên Việt Nam khối chuyên tin năm 2021 dưới đây nhé.
Đề thi Olympic tin học sinh viên Việt Nam khối chuyên tin năm 2021
Đề thi bao gồm 4 bài, và tổng số trang là 5, mỗi một bài sẽ tương ứng với 100 điểm và bao gồm 50 test, tức là bạn vượt qua mỗi test sẽ được tính 2 điểm, và vượt được test nào thì sẽ tính điểm test đấy không yêu cầu phải giải chính xác cả 50 test mới tính điểm.
Cụ thể đề thi mình có chụp lại ảnh bên dưới(Ảnh tương đối mờ bạn chịu khó đọc một chút nhé).





Ý tưởng giải bài 1(Truy vết)
Đề thì loàng ngoằng khó hiểu vậy thôi, nhưng tóm lại bản chất của bài toán này chỉ là đi tính khoảng cách trong hệ trục tọa độ.
Cụ thể ý tưởng bài toán sẽ là từ tọa độ vị trí của F0, duyệt 1 vòng lặp đề tìm ra các F1 có khoảng cách với F0 là nhỏ hơn khoảng cách D.
- Kiếm tiền Accesstrade, kiếm tiền tại nhà với Accesstrade.vn – Tiếp thị liên kết
- MegaURL – Rút gọn link kiếm tiền có giá cao tại Việt Nam
- Top 4 App kiếm tiền online trên điện thoại tốt nhất 2022
Tiếp tục, duyệt 2 vòng, với vòng lặp thứ nhất sẽ duyệt lần lượt các F1, vòng lặp thứ 2 sẽ kiểm tra khoảng cách của F1 thứ i với những người chưa tiếp xúc tính khoảng cách có nhỏ hơn khoảng cách D không để tìm ra các F2.
Mỗi lần tìm ra được F1, F2 chúng ta cần đánh dấu lại là người này đã tiếp xúc, để làm được việc này chúng ta sẽ cần thêm 1 mảng gọi là mảng đánh dấu.
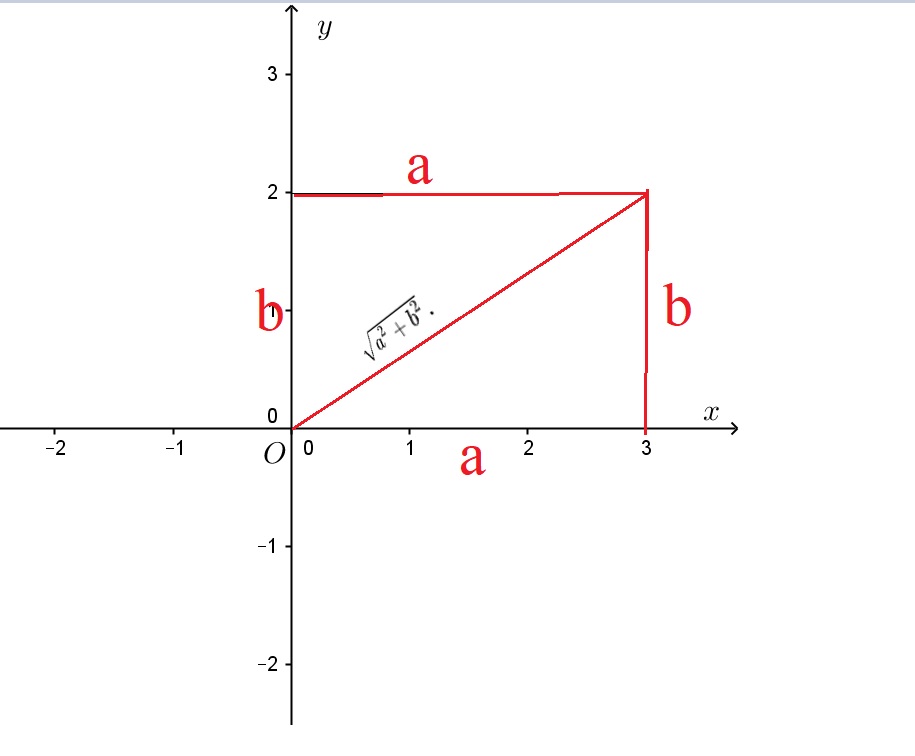
Công thức để tính được khoảng cách trong hệ trục tọa độ thì bản chất nó cũng chỉ là định lý Pythagoras(pi-ta-go). Và độ dài a, b sẽ là x2-x1, và y2-y1.
Code minh họa
#include <bits/stdc++.h>
using namespace std;
int dd[1001]= {0};
int F1, F2;
int tinhKhoangCach(int a[], int b[])
{
return sqrt(pow(b[0] - a[0], 2) + pow(b[1] - a[1], 2));
}
void truyVet(int a[][2], int n, int d, int f0)
{
for(int i = 1;i<=n;i++)
{
if(dd[i] == 0 && tinhKhoangCach(a[f0], a[i]) < d)
{
F1++;
dd[i] = 1;
}
}
for(int i = 1;i<=n;i++)
{
if(dd[i] == 1) for(int j=1;j<=n;j++)
{
if(dd[j] == 0 &&tinhKhoangCach(a[i], a[j]) < d)
{
F2++;
dd[j]=3;
}
}
}
}
int main()
{
int n, f0, d;
cin>>n>>f0>>d;
int a[n+1][2];
for(int i=1;i<=n;i++)
{
cin>>a[i][0]>>a[i][1];
}
dd[f0] = 2;
truyVet(a, n,d,f0);
cout<<F1<<" "<<F2;
return 0;
}
Ý tưởng giải bài 3(Cầu kính)
Bài này ý tưởng cũng cực kì đơn giản, gọi mỗi cây cầu được cấu tạo từ 2 xâu a, b. Với 1 biến kết quả khởi tạo giá trị bằng 1(Vì nếu là 0 kết quả khi nhân vào sẽ bị bằng 0).
Duyệt 2 xâu từ đầu xâu tới cuối xâu, nếu tại vị trí i cả 2 xâu đều là X, thì robot sẽ có 2 cách di chuyển, vậy chúng ta sẽ nhân đôi kết quả lên.
Nếu tại vị trí i, 1 xâu là X, 1 xâu là O thì tức là robot chỉ có thể có 1 cách di chuyển, vậy kết quả tại vị trí này giữ nguyên không cần làm gì cả(chương trình bên dưới mình bỏ qua luôn).
Nếu tại vị trí i, cả 2 xâu đều là O, lúc này robot không có cách di chuyển. Có thể dừng vòng lặp lập tức và in ra kết quả bằng 0.
Lưu ý là đề yêu cầu là đưa ra kết quả chia dư cho 10^7 vì nếu có nhiều cặp XX thì kết quả sẽ cứ nhân đôi lên con số sẽ cực lớn. Bạn phải chia dư ngay bên trong vòng lặp mỗi lần nhân đôi kết quả, nếu không là sẽ bị tràn số.
Code minh họa
#include <bits/stdc++.h>
using namespace std;
int mod = 1000000007;
int kq;
int main()
{
int n; cin>>n;//Nhập n cầu
string a, b;
for(int i=0;i<n;i++)
{
cin>>a>>b;//Nhập cầu thứ i
int length = a.length(); //Vì chắc chán độ dài a sẽ luôn bằng b nên chỉ cần lấy độ dài a hoặc b
kq = 1; //Khởi tạo lại biến k1 = 1
//Vòng lặp xử lý kết quả cây cầu thứ i
for(int j=0; j<length; j++)
{
if(a[j] == 'X' && b[j] == 'X') kq *=2;//Nếu cặp XX nhân đối kq
//Nếu cặp O O kq = 0 và dừng vòng lặp
else if(a[j] == 'O' && b[j] == 'O'){
kq = 0;
break;
}
kq %= mod; //Chia dư kq cho 10^7 bên trong vòng lặp j để tránh tràn số
}
//in kết quả cây cầu thứ i
cout<<kq<<"\n";
}
}
Hai bài còn lại thì thuật toán của mình cũng không được tốt cho lắm nên chưa có ý tưởng :)), bạn nào có ý tưởng để lại comment bên dưới để mọi người cùng học hỏi nhé!.
XÊM THÊM Cách tìm UCLN và BCNN trong lập trình C/C++ Thuật toán tìm kiếm nhị phân trong C/C++ Thuật toán đếm số lượng chữ số của số nguyên dương n bằng C / C++ Thuật toán sắp xếp nhanh (Quick Sort)

Bình luận