Trong viết viết trước chúng ta đã cùng nhau tìm hiểu và làm bài tập cũng như viết hàm tìm Ước số chung lớn nhất của 2 số nguyên dương, trong bài viết này chúng ta tiếp tục làm một dạng bài tập liên quan tới UCLN nhất.
Tuy nhiên, trong bài này chúng ta sẽ làm nâng cao lên một chút. Không chỉ đi tìm ước chung lớn nhất của 2 số nữa, mà chúng ta sẽ tìm ước chung của 3 số, 4 số, hoặc rất nhiều số, hoặc là cả 1 mảng gồm n số.
Ý tưởng cách tìm ƯCLN của nhiều số
Trong bài viết trước ta đã có hàm tìm ước chung lớn nhất của 2 số nguyên như sau:
int GCD(int a, int b){
if(b==0) return a; //Sau đệ quy lúc này kiểm tra b chính là a%b được truyền vào tức nó chính là r, còn a chính là b được truyền vào
return GCD(b, a%b); // Gọi lại hàm đệ quy tính UCLN giữa b và r
}
(Tìm UCLN sử dụng giải thuật Euclid và hàm đệ quy)
Và bội chung nhỏ nhất của 2 số thì chính bằng tích của 2 số đó chia cho ƯCLN của 2 số đó, vậy mình sẽ viết lại hàm tìm BCNN như sau:
int BCNN(int a, int b){
int tich = a*b; //Tính tích của a nhân B
int ucln = GCD(a,b); //Tìm ước chung lớn nhất của a, b (Gọi hàm GCD bên trên)
return tich/ucln; //trả về cho hàm kq tích a*b chia cho ucln(a,b)
}
*Ý tưởng tìm ƯCLN và BCNN của nhiều số*
Để tìm ƯCLN của nhiều số, ta sẽ tìm ước chung lớn nhất của 2 số, sau đó coi kết quả đó là 1 số, và tiếp tục thực hiện tìm ước chung lớn nhất của kq đó với 1 số tiếp theo cho đến khi hết tất cả dãy số cần tìm ước chung.
Ví dụ: Ta sẽ tìm Ưcln của 24, 16, 6, 2
Bước 1: Tìm ƯCLN của 24 và 16 được kết quả là 8.
Bước 2: Lấy kq là 8 tiếp tục tìm ucln giữa kq đó và số tiếp theo trong dãy, tức là tìm ucln của 8 và 6 được kết quả là 2.
Bước 3: Tìm ucln giữa kq bước trước là 2, và số tiếp theo là 2 => ucln của hai số này chính là 2.
=> Vậy UCLN của bốn số là 24, 16, 6, 2 là 2.
Tìm bội chung nhỏ nhất ta làm tương tự như vậy.
Code minh họa cho thuật toán
Tìm UCLN và BCNN của 4 số
(3 số, 5 số, 6 số....ta làm tương tự chỉ cần nhập thêm hoặc bất đi 1 biến số)
Code minh họa tìm UCLN
#include <stdio.h>
//Hàm tìm UCLN của 2 số nguyên
int GCD(int a, int b){
if(b==0) return a;
return GCD(b, a%b);
}
int main()
{
int a, b, c, d; /Khai báo 4 số
printf("Nhap a: "); scanf("%d", &a);
printf("Nhap b: "); scanf("%d", &b);
printf("Nhap c: "); scanf("%d", &c);
printf("Nhap d: "); scanf("%d", &d);
int kq = GCD(a,b);//Tìm ucln của 2 số a,b
kq = GCD(kq,c); //Tìm ucln của kq trước với c
kq = GCD(kq,d); //Tìm ucln của kq với d
printf("%d", kq);//In kết quả tìm được
}
Kết quả thực hiện chương trình
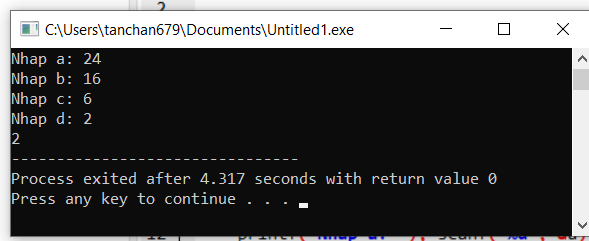
Vậy chương trình in ra kết quả là 2, đúng với ví dụ mình minh họa bên trên.
Code minh họa tìm BCNN
#include <stdio.h>
//Hàm tìm ucln của 2 số
int GCD(int a, int b){
if(b==0) return a;
return GCD(b, a%b);
}
//Hàm tìm BCNN của 2 số
int BCNN(int a, int b){
int tich = a*b;
int ucln = GCD(a,b);
return tich/ucln;
}
int main()
{
int a, b, c, d;
printf("Nhap a: "); scanf("%d", &a);
printf("Nhap b: "); scanf("%d", &b);
printf("Nhap c: "); scanf("%d", &c);
printf("Nhap d: "); scanf("%d", &d);
int kq = BCNN(a,b); //Tìm bcnn của , b
kq = BCNN(kq,c); //Tìm bcnn của k1 bước trước với c
kq = BCNN(kq,d); //Tương tự
printf("%d", kq); //In kết quả
}
Kết quả thực hiện chương trình

Tìm UCLN và BCNN của một mảng
Code mẫu tìm ƯCLN của một mảng
#include <stdio.h>
//Hàm tính ucln của 2 số
int GCD(int a, int b){
if(b==0) return a;
return GCD(b, a%b);
}
//Hàm tìm UCLN của một mảng a gồm n phần từ
int GCD_Array(int n, int a[]){
int kq = a[0];//Gan k1 bằng pt đầu tiên
for(int i = 1; i < n; i++){
kq = GCD(kq, a[i]); //Tìm ucln của kq với số tiếp theo trong mảng
}
return kq;//Trả về k1 cho hàm
}
int main()
{
int n;
printf("Nhap so phan tu: ");
scanf("%d", &n); //Nhap n phân tử cho mảng
//Khai báo mảng a gồm n phần tử
int a[n];
//Nhập vào mảng a
for(int i = 0;i<n;i++){
printf("a[%d] = ", i);
scanf("%d", &a[i]);
}
int kq = GCD_Array(n, a );//Tìm kq UCLN của mảng
printf("%d", kq); //In kết quả
}
Kết quả khi chạy chương trình
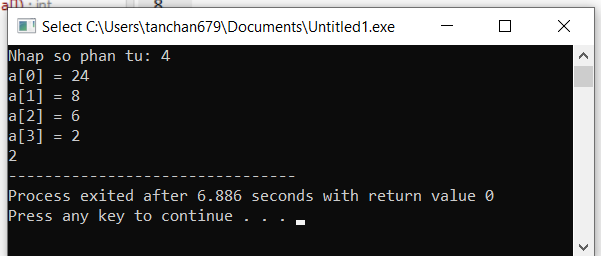
Code mẫu tìm BCNN của một mảng
#include <stdio.h>
int GCD(int a, int b){
if(b==0) return a;
return GCD(b, a%b);
}
int BCNN(int a, int b){
int tich = a*b;
int ucln = GCD(a,b);
return tich/ucln;
}
int BCNN_Array(int n, int a[]){
int kq = a[0];
for(int i = 1; i < n; i++){
kq = BCNN(kq, a[i]);
}
return kq;
}
int main()
{
int n;
printf("Nhap so phan tu: ");
scanf("%d", &n);
int a[n];
for(int i = 0;i<n;i++){
printf("a[%d] = ", i);
scanf("%d", &a[i]);
}
int kq = BCNN_Array(n, a);
printf("%d", kq);
}
Kết quả khi chạy chương trình
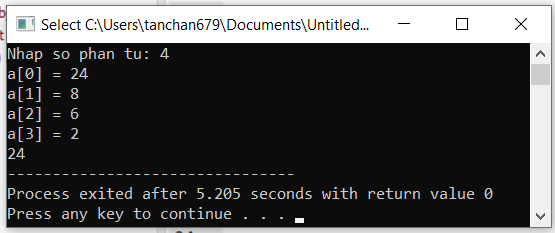
[XEM THÊM NHIỀU BÀI VIẾT LẬP TRÌNH C/C++ TẠI ĐÂY]
XEM THÊM Thuật toán tìm kiếm nhị phân trong C/C++ Thuật toán tính dãy số Fibonacci bằng 3 cách trong C/C++ Thuật toán đếm số lượng chữ số của số nguyên dương n bằng C / C++ Thuật toán sắp xếp nhanh (Quick Sort)

Bình luận