DANH SÁCH BÀI VIẾT Tìm hiểu thuật toán Quy hoạch động Tìm hiểu về Hàm đệ quy Thuật toán tìm kiếm nhị Tìm hiểu về Thuật toán quay lui (Backtracking) Tìm hiểu thuật toán Loang Tìm hiểu thuật toán chia để trị Tìm hiểu thuật toán tham lam trong lập trình Giải thuật tìm kiếm theo chiều sâu DFS (Depth First Search) Giải thuật tìm kiếm theo chiều rộng BFS (Breadth-first search) Tìm hiểu về thuật toán Sàng nguyên tố (sàng Eratosthenes)
Bài viết trước chúng ta đã cùng tìm hiểu về giải thuật Tìm kiếm theo chiều sâu DFS (Depth First Search), trong bài viết này chúng ta sẽ tiếp tục tìm hiểu thêm một giải thuật hay dùng trong duyệt đồ thị và duyệt cây là Tìm kiếm theo chiều rộng BFS(Breadth-first search).
Theo dõi thêm các bài viết sau mình sẽ có các bài toán áp dụng giải thuật này.
Giải thuật tìm kiếm theo chiều rộng BFS.
Giải thuật tìm kiếm theo chiều rộng (Breadth-First Search – viết tắt là BFS), còn được gọi là giải thuật tìm kiếm ưu tiên chiều rộng, là giải thuật duyệt hoặc tìm kiếm trên một cây hoặc một đồ thị.
Không giống như DFS từ một đỉnh gốc khi tìm được 1 đỉnh con(nút con trên cây hay còn gọi là cành), thuật toán sẽ ngay lập tức chuyển qua đỉnh tiếp theo và thực hiện lặp lại cho tới khi đỉnh đó không còn đỉnh con nào thì quay lui lại 1 bước trước đó tìm kiếm các đỉnh liên kề con khác.
Giải thuật BFS từ một đỉnh gốc sẽ duyệt qua tất cả các đỉnh con liền kề (nút con trên cây) của đỉnh đó. Lưu các đỉnh con liền kề vào stack, sau đó từ các đỉnh con này ta lại tiếp tục thực hiện tìm kiếm tất cả các đỉnh con của các đỉnh con đó(đỉnh cháu của nút gốc).Cứ thực hiện lặp như vậy cho tới khi nào không con một nút con trong cây hoặc đồ thị khi đó giải thuật kết thúc.
Thực hiện trên đồ thị với mỗi đỉnh duyệt qua ta sẽ cần đánh dấu nó lại tránh trường hợp ta duyệt qua đỉnh đó nhiều lần. Vì trên đồ thị rất có thể các đỉnh con sẽ lại liên kết lại với các nút nằm trước đó.
Xem hình minh họa dưới đây để hiểu hơn.

Với hình minh họa trên là chúng ta đang đi tìm kiếm phần tử 13, vì thế nên sau khi tìm được phần tử đó giải thuật sẽ kết thúc. Nhưng nếu giải thuật chúng ta là duyệt tất cả phần tử trong cây thì ta chỉ việc bỏ điều kiện dừng, khi đó duyệt hết các phần tử trong cây giải thuật sẽ tự kết thúc.
Duyệt trên đồ thị, với hình minh họa mình vẽ bên dưới mình sẽ lấy đỉnh A làm đỉnh gốc để duyệt nhé, tất nhiên có thể lấy đỉnh khác làm gốc vì trên đồ thị thì không có khái niệm đỉnh gốc cả, đỉnh nào cũng là con mà đỉnh nào cũng là gốc. Thứ tự duyệt đồ thị sẽ như sau.
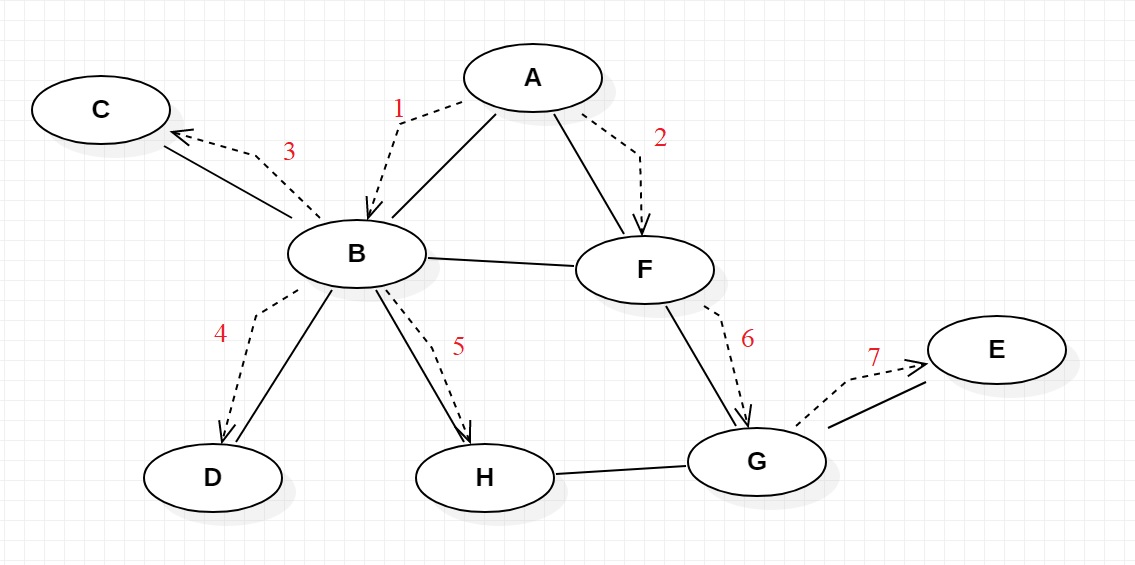
Khi xuất phát từ A, các đỉnh con của A là B, F. Tiếp tục duyệt các nút con B là C, D, H và của F là G. Các đỉnh C, D không liên kết tới đỉnh nào, đỉnh H liên kết tới G nhưng đỉnh G đã được duyệt trước đó. Và đỉnh G sẽ có con là E.
Tóm lại các bước duyệt qua các đỉnh sau:
Bước 1: Đỉnh A
Bước 2: Đỉnh, B, F
Bước 3: Đỉnh C, D, H, G
Bước 4: Đỉnh E
Minh họa giải thuật
Chương trình dưới đây sẽ cho nhập vào một ma trận đồ thị sau đó dyệt qua tất cả các đỉnh của đồ thị. Vì là nhập ma trận đồ thị nên số lượng nhập sẽ tương đối nhiều vì thế chương trình sẽ lấy dữ liệu từ file input.txt,, trước khi chạy chương trình cần tạo file input.txt với dữ liệu hàng 1 ghi 1 số là số lượng đỉnh, và n*n hàng tiếp theo biểu diễn ma trận đồ thị.
#include<iostream>
#include<conio.h>
using namespace std;
#define MAX 100
#define TRUE 1
#define FALSE 0
int G[MAX][MAX], n, chuaxet[MAX], QUEUE[MAX];
void Init(){
freopen("input.txt","rt",stdin);
cin>>n;
cout<<"So dinh cua do thi n = "<<n<<endl;
//nhap ma tran lien ke.
for(int i=1; i<=n;i++){
for(int j=1; j<=n;j++){
cin>>G[i][j];
}
}
for(int i=1; i<=n;i++){
chuaxet[i]=TRUE;
}
}
/* Breadth First Search */
void BFS(int i){
int u,dauQ, cuoiQ;
dauQ=1; cuoiQ=1;QUEUE[cuoiQ]=i;chuaxet[i]=FALSE;
/* thi?t l?p hàng d?i v?i d?nh d?u là i*/
while(dauQ<=cuoiQ){
u=QUEUE[dauQ];// l?y d?nh u ra kh?i queue.
cout<<"duyet qua dinh: "<<(char(u+64))<<endl;
dauQ=dauQ+1; /* duy?t d?nh d?u hàng d?i*/
for(int j=1; j<=n;j++){
if(G[u][j]==1 && chuaxet[j] ){
cuoiQ=cuoiQ+1;
QUEUE[cuoiQ]=j;
chuaxet[j]=FALSE;
}
}
}
}
int main(){
Init();
for(int i=1; i<=n; i++)
if (chuaxet[i])
BFS(i);
_getch();
}
Với ví dụ đồ thị minh họa ở phía trên chúng ta có ma trận đồ thị như sau.
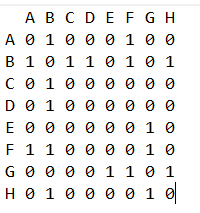
Như vậy file input.txt sẽ có dữ liệu như sau(Tạo file và coppy dữ liệu này chạy thử với chương trình):
8
0 1 0 0 0 1 0 0
1 0 1 1 0 1 0 1
0 1 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
1 1 0 0 0 0 1 0
0 0 0 0 1 1 0 1
0 1 0 0 0 0 1 0Và đây là kết quả khi thực thi chương trình, thứ tự duyệt nó hoàn toàn khớp với những gì mô tả ở minh họa bên trên.
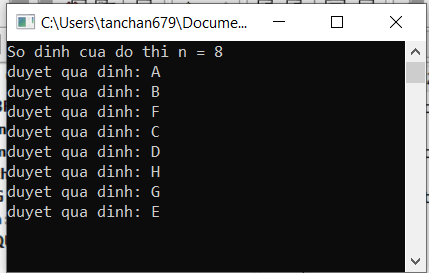
Cảm ơn bạn đã đọc bài viết chúc bạn học tốt! sớm trở thành một Pro Dev.
[Xem tất cả bài viết chủ đề C/C++ tại đây]

Bình luận