DANH SÁCH BÀI VIẾT Giải thuật tìm kiếm theo chiều rộng BFS (Breadth-first search) Giải thuật tìm kiếm theo chiều sâu DFS (Depth First Search) Duyệt đồ thị, tìm kiếm đường đi dài nhất, đường đi ngắn nhất trong đồ thị Kiểm tra đồ thị liên thông trong bài toán đồ thị lập trình
Trong bài viết này chúng ta sẽ cùng làm các bài tập liên quan tới đồ thị là duyệt đồ thị, tìm kiếm đường đi dài nhất từ một đỉnh tới một đỉnh khác, tìm kiếm đường đi ngắn nhất từ một đỉnh này tới một đỉnh khác.
Với bài viết này mình sẽ sử dụng ngôn ngữ lập trình C/C++.
Duyệt đồ thị
Với yêu cầu duyệt đồ thị tức là chúng ta sẽ duyệt qua tất cả các đỉnh của đồ thị và in mỗi đỉnh được duyệt qua ra qua ra màn hình.
Với cả 3 ý là duyệt đồ thị, tìm kiếm đường đi dài nhất, đường đi ngắn nhất mình đều sử dụng cách nhập vào đồ thị là một ma trận đồ thị.
Vậy mình sẽ có trước một đồ thị minh họa như sau.

Như vậy ma trận đồ thị cho đồ thị trên như bên dưới.(A, B, C...G, H tương ứng với các đỉnh từ 1 tới 8)
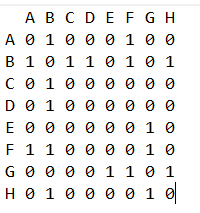
Mình viết lại dưới đây cho bạn dễ coppy, với dòng đầu tiên n là số lượng đỉnh, n*n dòng tiếp theo biểu diễn ma trận đồ thị.
8
0 1 0 0 0 1 0 0
1 0 1 1 0 1 0 1
0 1 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
1 1 0 0 0 0 1 0
0 0 0 0 1 1 0 1
0 1 0 0 0 0 1 0Với tất cả các ví dụ bên dưới mình sẽ sử dụng ma trận đồ thị này để chạy mẫu chương trình!.
Duyệt đồ thị bằng giải thuật DFS
Nếu bạn vẫn chưa biết giải thuật DFS thì xem bài viết này nhé: Giải thuật tìm kiếm theo chiều sâu DFS (Depth First Search).
Với giải thuật này, duyệt đồ thị ta sẽ viết code như sau:
#include <iostream>
#include <algorithm>
using namespace std;
bool dd[1000]; //Mảng đánh dấu đỉnh ma trận
int dem=1, n;
int a[1000][1000]; //Ma trận đồ thị
int b[1000]; //Mảng để lưu thứ tự duyệt đồ thị
//Hàm duyệt đồ thị sử dụng giải thuật DFS
void duyetDoThi(int i)
{
//Vòng for để duyệt qua tất cả các đỉnh
for(int j=1;j<=n;j++)
{
if(a[i][j] != 0 && dd[j]==0)//Neus có đường đi từ đỉnh i tới đỉnh j và đỉnh j chưa đươc duyệt
{
dd[j ]= 1; //Đánh dấu đỉnh j được duyệt
b[dem++] = j; //Cho đỉnh j vào mảng b để lát nữa ta in ra thứ tự duyệt
duyetDoThi(j); //đệ quy với đỉnh tiếp theo
}
}
}
//Hàm in thứ tự duyệt đồ thị
void inDoThi(){
for(int i = 0;i<n;i++) cout<<b[i]<<" ";
}
int main()
{
cout<<"nhap so dinh: "; cin>>n;
cout<<"Nhap ma tran do thi: \n";
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>a[i][j];
cout<<"Ma tran do thi: \n";
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
cout<<a[i][j]<<" "; cout<<endl;
}
cout<<"\n\nDuyet do thi: ";
b[0] = 1; //Lấy đỉnh 1 là đỉnh gốc nên ta gắn b 0 là đỉnh 1 để lát nữa ta in ra thứ tự duyệt đồ thị
dd[1] = 1;//Đánh dấu đỉnh 1 đã được duyệt
duyetDoThi(1); //Gọi duyệt đồ thị
inDoThi(); //in ra thứ tự duyệt đồ thị
}
Kết quả duyệt đồ thị theo giải thuật DFS.

Như vậy kết quả duyệt đồ thị qua các đỉnh theo thứ tự duyệt DFS sẽ là: 1 - 2 - 3 - 4 - 6 - 7 - 5 - 8(Xem lại hình minh họa phía trên xem thứ tự duyệt như thế nào nhé).
Biểu diễn lại trên hình vẽ(màu xanh ra trời, số màu đỏ là thứ tự).

Duyệt đồ thị bằng giải thuật BFS
Nếu bạn vẫn chưa biết giải thuật BFS thì xem bài viết này nhé: Giải thuật tìm kiếm theo chiều rộng BFS (Breadth-first search).
Với giải thuật này, duyệt đồ thị ta sẽ viết code như sau:
#include<iostream>
#include<conio.h>
using namespace std;
#define MAX 100
#define TRUE 1
#define FALSE 0
int G[MAX][MAX], n, chuaxet[MAX], QUEUE[MAX];
void Init(){
cin>>n;
cout<<"So dinh cua do thi n = "<<n<<endl;
//nhap ma tran lien ke.
for(int i=1; i<=n;i++){
for(int j=1; j<=n;j++){
cin>>G[i][j];
}
}
for(int i=1; i<=n;i++){
chuaxet[i]=TRUE;
}
}
/* Breadth First Search */
void BFS(int i){
int u,dauQ, cuoiQ;
dauQ=1; cuoiQ=1;QUEUE[cuoiQ]=i;chuaxet[i]=FALSE;
/* thi?t l?p hàng d?i v?i d?nh d?u là i*/
while(dauQ<=cuoiQ){
u=QUEUE[dauQ];// l?y d?nh u ra kh?i queue.
cout<<" "<<(u);
dauQ=dauQ+1; /* duy?t d?nh d?u hàng d?i*/
for(int j=1; j<=n;j++){
if(G[u][j]==1 && chuaxet[j] ){
cuoiQ=cuoiQ+1;
QUEUE[cuoiQ]=j;
chuaxet[j]=FALSE;
}
}
}
}
int main(){
Init();
cout<<"\n\nKet qua duyet BFS:\n";
for(int i=1; i<=n; i++)
{
if (chuaxet[i]) BFS(i);
}
_getch();
}
Kết quả duyệt đồ thị theo giải thuật BFS.
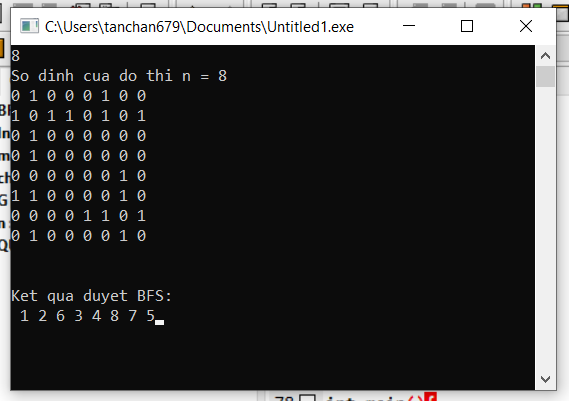
Như vậy kết quả duyệt đồ thị qua các đỉnh theo thứ tự duyệt DFS sẽ là: 1 - 2 - 6 - 3 - 4 - 8 - 7 - 5.
Biểu diễn lại trên hình vẽ(màu xanh ra trời, số màu đỏ là thứ tự).

Tìm đường đi dài nhất
Để tìm đường đi dài nhất hoặc ngắn nhất trong đồ thị ta sẽ kết hợp giữa giải thuật duyệt DFS, và thuật toán quay lui(Backtracking).
Với ví dụ này ta sẽ nhập vào ma trận đồ thị, và 2 đỉnh u và v. Sau đó tìm đường đi dài nhất từ u tới v.
Ý tưởng của bài toán tìm đường đi dài nhất sẽ là tìm kiếm tất cả các đường đi từ đỉnh u tới v có thể đi được. Sau đó ta đem so sánh đường đi nào là dài nhất.
Chương trình
#include <iostream>
#include <algorithm>
using namespace std;
bool dd[1000], tt = 0; //Mảng đánh dấu tối đa 1000 đỉnh
int dem=1,dem2, n;// dem sử dụng để đếm số bước đi của đường đi hiện tai, dem2 để lưu số bước của đường đi dài nhát trước đó
int a[1000][1000]; //Mảng để lưu mảng đồ thị
int b[1000], c[1000]; //Mảng c để lưu đường đi dài nhất tìm được tạm thời, mảng b sử dụng trong qua trình tìm 1 đường đi
int u,v; //2 đỉnh u và v
//Hàm tìm đường đi dài nhất
void duongdidainhat(int i)
{
dd[i]=1; //Đánh dấu đỉnh i đã đi qua
//Nếu đinh i chính bằng v tức là từ đỉnh u ta đã đi tới v
if(i==v)
{
tt=1;
//Phần này chính là vét cạn đó, ta tìm tất cả đường đi rồi so sánh lấy được đường đi dài nhất
//Nếu đường đi hiện tại tìm được lớn hơn đường đi dài nhất ban đầu
if(dem > dem2)
{
//Gắn đường đi dài nhất bằng đường đi tìm được, gắn lại biến đếm
for(int j=0;j<dem;j++) c[j]=b[j]; dem2 = dem;
}
}
//Nếu chưa tới đỉnh v ta tiếp tục duyệt các đỉnh chưa đi qua
else for(int j=0;j<n;j++)
{
if(a[i][j] != 0 && dd[j]==0)//Kiểm tra xem giữa 2 đỉnh có tồn tại đường đi không, và đỉnh đó đã đi qua trước đó chưa
{
b[dem++] = j; //Tăng biến đếm bước đi lên 1, đồng thời gắn đường đi tại đỉnh j
duongdidainhat(j); //duyệt đỉnh j tiếp tục tìm kiếm đường đi
dem--; dd[j]=0;//Thoát khỏi hàm quay lui, lúc này hàm quay lui sẽ lùi về 1 bước phía trước, và tìm kiếm 1 đường đi khác có thể sảy ra.....ta trừ đi biến đếm 1 đơn vị và gắn lại đỉnh đó là chưa đi qua
}
}
}
//Hàm hiển thị đường đi
void induongdi()
{
for(int i = 0;i<dem2; i++) cout<<c[i] + 1<<" ";
}
int main()
{
cout<<"nhap so dinh: "; cin>>n;
cout<<"Nhap ma tran do thi: \n";
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin>>a[i][j];
cout<<"Ma tran do thi: \n";
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
cout<<a[i][j]<<" "; cout<<endl;
}
cout<<"Nhap dinh u "; cin>>u;
cout<<"Nhap dinh v "; cin>>v;
u = u - 1; v = v - 1;//Vì đỉnh mình quy ước tương ứng từ 1, mà ma trận mình cho nhập từ 0 nên ta lấy đỉnh trừ đi 1 sẽ đúng ví trí trong ma trận
b[0]=u;
duongdidainhat(u);
if(tt) induongdi(); else cout<<"Kg ton tai duong di tu u toi v";
}
Kết quả thực hiện chương trình với đồ thị trên và đi từ đỉnh 1 tới đỉnh 3.

Vậy đường đi dài nhất thuật toán tìm được khi đi từ đỉnh 1 tới 3 là: 1 - 6 - 7 - 8 - 2 -3.
Biểu diễn trên hình vẽ(đường mau xanh).

Thách bạn tìm được cách đi nào từ 1 tới 3 mà dài hơn nữa đấy :))) tìm được thì thuật toán mình sai:)).
Tìm đường đi ngắn nhất
Ý tưởng của bài toán tìm đường đi ngắn nhất từ đỉnh u tới v tương tự như tìm kiếm đường đi dài nhất. Thay vì so dánh xem đường đi nào dài nhất ta sẽ so sánh xem đường đi nào ngắn nhất, tức là ta có thể coppy đoạn code trên và chỉ cần thay thế dấu so sánh từ lớn hơn thành dấu bé hơn trong đoạn code khi tìm được 1 đường đi là được
Vậy ta sửa lại code như sau:
#include <iostream>
#include <algorithm>
using namespace std;
bool dd[1000], tt = 0;
int dem=1,dem2=99999999, n; //Gắn dem2 là một số rất lớn để lát nữa tìm được đường đi đầu tiên ta đem đương đi ngắn nhất so sánh với đếm này.
int a[1000][1000];
int b[1000], c[1000];
int u,v;
void duongDiNganNhat(int i)
{
dd[i]=1;
if(i==v)
{
tt=1;
if(dem < dem2) //Chỉ cần đổi dấu ở chỗ này là ta đã được thuật toán tìm đường đi ngắn nhất rồi.
{
for(int j=0;j<dem;j++) c[j]=b[j]; dem2 = dem;
}
}
else for(int j=0;j<n;j++)
{
if(a[i][j] != 0 && dd[j]==0)
{
b[dem++] = j;
duongdidainhat(j);
dem--; dd[j]=0;
}
}
}
void induongdi()
{
for(int i = 0;i<dem2; i++) cout<<c[i] + 1<<" ";
}
int main()
{
cout<<"nhap so dinh: "; cin>>n;
cout<<"Nhap ma tran do thi: \n";
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin>>a[i][j];
cout<<"Nhap dinh u "; cin>>u;
cout<<"Nhap dinh v "; cin>>v;
u = u - 1; v = v - 1;
b[0]=u;
duongDiNganNhat(u);
if(tt) induongdi(); else cout<<"Kg ton tai duong di tu u toi v";
}
Kết quả thực hiện chương trình với đồ thị trên và vẫn là đi từ đỉnh 1 tới đỉnh 3.
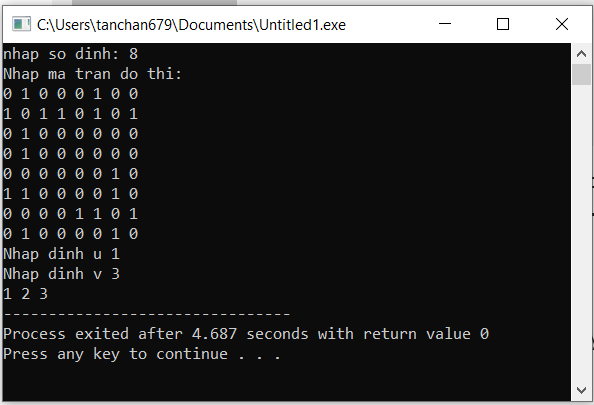
Vậy đường đi ngắn nhất thuật toán tìm được khi đi từ đỉnh 1 tới 3 là: 1 - 2 - 3(A - B - C).
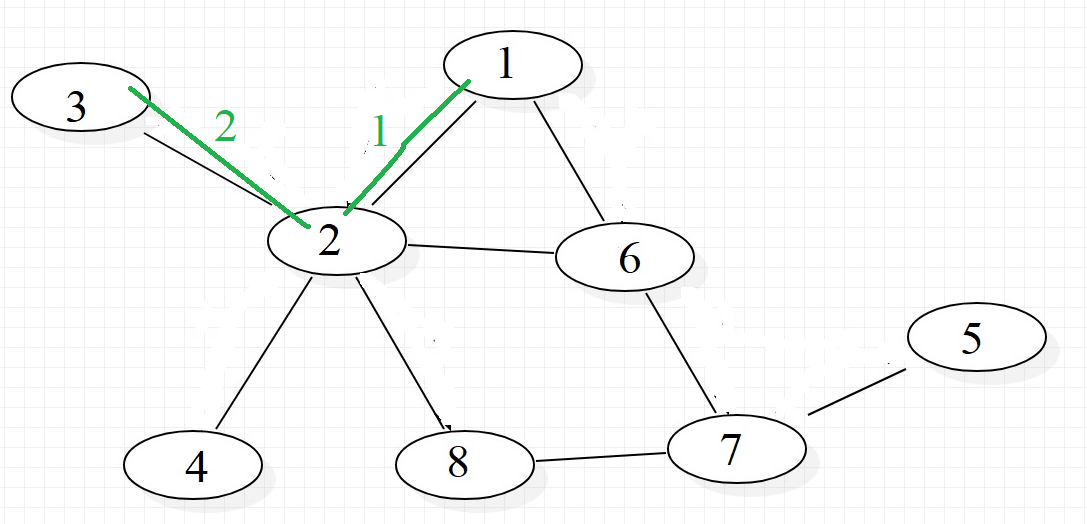
Biểu diễn trên hình vẽ(đường màu xanh).
Cảm ơn bạn đã đọc bài viết chúc bạn học tốt! sớm trở thành một Pro Dev.
[Xem tất cả bài viết chủ đề C/C++ tại đây]

Bình luận